티스토리 뷰
>문제

> 핵심
최빈값 출력
시간복잡도 O(n^2) 사용 X -> (이중반복문 X)
반올림
>풀이과정
쉬울줄 알았는데..
최빈값 출력때문에 골탕먹었다.
1. 산술평균
N개의 수들의 합을 N개로 나는 값. 그냥 우리가 평소에 나누기 하는 방식이 산술평균이다.
이거 보니까 이 문제랑 관련은 없는데 고딩때 배운 산술기하 평균이 생각나서 다시 한번 찾아봤다.
· 산술평균 (Arithmetic mean) -> 합의 평균, 우리가 평소에 평균내는 일상적인 방식
· 기하평균 (Geometric Mean)-> 곱의 평균, 비율평균, 각 요소를 곱한 후 n 제곱근을 씌운 값.
물가상승률이나 투자 수익률 계산에 쓰인다.
비트코인에 100만원을 투자하고 20% 수익을 낸 이후에 다른 코인에 투자했다가 20% 손실을 봤다고 가정하자,
이를 산술평균으로 구하면 +20% 상승에 -20% 하락이니 총 0%, 100만원 원금이 남는다고 나오는데 이는 틀렸다.
√(1.2 * 0.8) = 0.98 * 100만 => 98만원이 남게되고 나는 2만원 손실을 본 상황인 것이다!
내가 사실 그 상황이다.
1850원에 페이코인에 80만원을 넣어놓고 5% 수익을 봤다가 현재 10% 이상 손실을 보고있는 중이다..
눈물이 난다. 애초에 발을 들이지를 말았어야 하는데 꼼짝없이 고점에 물려있다. 수학이 곧 인생이다.
산술기하 평균 부등식은, 산술평균이 기하평균보다 항상 크거나 같다는 부등식이다.
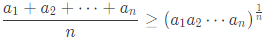
이게 중요한게 아닌데 잡소리가 길어졌다.
이 문제에서 산술평균을 구하는데 중점은 반올림 이다.
반올림 방법은 여러가지가 있다.
1. <math.h> 에 포함된 올림 / 반올림 / 내림 함수 사용
· 올림 : ceil(double_X)
· 반올림 : round(double_X)
· 내림 : floor(double_X)
int arith(int list[], int n)
{
double sum = 0;
for (int i = 0; i < n; i++)
{
sum += (list[i]);
}
return round(sum / n);
}2. 0.5 더하기
C언어에서 int 연산을 하면 내림연산을 한다
4.4 + 0.5 = 4.9 내리면 4.
4.5 + 0.5 = 5.0 이니까 5.
4.6 + 0.5 = 5.1 내리면 5.
0.5만 더해줘도 반올림한 효과가 나는 것이다. 꼼수라면 꼼수랄까?
실수형으로 연산을 한 뒤 (int)로 형변환을 해서 출력하는것이다..
그리고 실수형 연산을 할 때, float 보다 double형을 사용하는 습관을 들이자!
float는 소숫점 6자리밖에 표현이 안되기때문에 정확한 연산을 위해서는 double!
int arith(int list[], int n)
{
double sum = 0;
for (int i = 0; i < n; i++)
{
sum += (list[i]);
}
sum /= n;
if (sum < 0)
sum -= 0.5;
else
sum += 0.5;
return (int)sum;
}3. %.0f 사용하기
%f 는 실수형을 출력하는데, 소숫점 아래 자릿수만큼 %.뒤에 붙이면 소숫점 자리수에서 반올림하여 출력한다
12.3456이 있다고 하면,
%.0f = 12
%.1f = 12.3
%.2f = 12.35
%.3f = 12.346 ...
자동 반올림이 된다. 이건 몰랐는데 앞으로 유용하게 쓰일 것 같다.
void arith(int list[], int n)
{
double sum = 0;
for (int i = 0; i < n; i++)
{
sum += (list[i]);
}
printf("%.0f\n", sum / n);
}
2. 중앙값
우선 중앙값을 구하기 전에 정렬이 필요하다.
이 문제에서는 O(n^2) 이상 사용하면 안되기 때문에 qsort 함수를 이용했다. (오름차순 정렬)
중앙값은 배열에서 정 가운데 있는 값이다.
요소의 개수가 짝수냐 홀수냐에 따라 계산방법이 살짝 다르다
· 홀수인 경우 : 3
1 2 3 4 5
· 짝수인 경우 : (3 + 4) / 2 = 3.5
1 2 3 4 5 6
이 문제에서는 요소의 개수가 홀수라고 했으니까, list[N/2] 번째 값을 출력하면 된다. ( 5/2 = 2.5 => list[2] = 3 )
원래 (N+1)/2 번째값이 중앙값인데 배열은 0부터 시작하므로 list[(N+1)/2 - 1] 로 푸는게 정석인 것 같긴 하다.
int median(int list[], int n)
{
if (n == 1)
return list[0];
else
return list[(n+1)/2 - 1];
}
3. 범위
범위는 그냥 최댓값 - 최솟값을 해주면 된다.
배열이 정렬되어있으므로 list[n-1] - list[0] 만 해주면 끝
int range(int list[], int n)
{
int max = list[n - 1];
int min = list[0];
return max - min;
}
4. 최빈값
얘가 이 문제의 핵심이다. 최빈값이 여러개 있을 경우 두번째로 작은 값을 출력해야한다.
처음에는 이중반복문을 돌면서 횟수를 일일히 카운트 하려고 했었는데 O(n^2) 의 시간이 소요되어 시간초과가 났다.
그래서 어떻게 해야하나.. 하다가 힌트를 좀 참고했다.
입력되는 정수가 절댓값 4000을 넘지 않는다.
그렇기 때문에 크기 8001 의 배열을 선언(-4000 ~ 4000, 0 포함!)한 후, 0부터 8001까지 반복문을 돌면서
list[입력값 + 4000]++ 을 하면서 채우는 방식을 이용했다.
-4000이 입력되면 list[0]++, 4000이 입력되면 list[8001]++ 이 되는 것.
그렇게 반복문을 한번 순회하면서 각 수가 몇번 등장했는지, 그리고 max값! 최대 몇번 등장했는지도 같이 찾는다.
그리고 다시 0부터 8001까지 반복문을 돌면서
max값이 두번 등장할때 인덱스 저장하고 break (-4000부터 4000까지 도는데 두번째로 작은 최빈값을 출력해야 하니까)
그리고 return (idx - 4000). (처음에 입력값 + 4000 했으니까)
아이고 어렵다.
이 문제를 풀다가 갑자기 코딩이 하기싫어져서 코자타임을 하루 가졌다.
다음주가 개강이라 백준 푸는 시간도 많이 줄어들 것 같다.
그래도 학기중에도 최소 하루 한문제는 푸는 것을 목표로 삼아야겠다.
>깨달은점
1. 실수형 연산을 할때는 float 보다는 double
2. 반올림 할때는 %.0f 로 출력을 때려버리는 방법도 있다
3. 입력되는 수의 범위가 크지 않을때는 배열을 활용하는 방법도 생각해보자
>코드
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int compare(const void* first, const void* second)
{
int* a = (int*)first;
int* b = (int*)second;
if (*a < *b)
return -1;
else if (*a > *b)
return 1;
else
return 0;
}
int arith(int list[], int n)
{
double sum = 0;
for (int i = 0; i < n; i++)
{
sum += (list[i]);
}
return round(sum / n);
}
int median(int list[], int n)
{
if (n == 1)
return list[0];
else
return list[(n + 1) / 2 - 1];
}
int Mode(int list[], int n)
{
int ar[8001] = { 0 };
int i, idx, max = 0, cnt = 0;
for (i = 0; i < n; i++)
{
idx = list[i] + 4000;
ar[idx] += 1;
if (ar[idx] > max)
max = ar[idx];
}
for (i = 0, idx = 0; i < 8001 ; i++)
{
if (ar[i] == 0)
continue;
if (ar[i] == max)
{
if (cnt == 0)
{
idx = i;
cnt += 1;
}
else if (cnt == 1)
{
idx = i;
break;
}
}
}
return idx - 4000;
}
int range(int list[], int n)
{
int max = list[n - 1];
int min = list[0];
return max - min;
}
int main()
{
int i, n;
int* list;
scanf("%d", &n);
list = (int*)calloc(n, sizeof(int));
for (i = 0; i < n; i++)
{
scanf(" %d", &list[i]);
}
qsort(list, n, sizeof(list[0]), compare);
printf("%d\n", arith(list, n));
printf("%d\n", median(list, n));
printf("%d\n", Mode(list, n));
printf("%d\n", range(list, n));
return 0;
}'알고리즘 > 기타' 카테고리의 다른 글
| [C] 백준 | 4949번 코드 - 균형잡힌 세상 (0) | 2021.02.27 |
|---|---|
| [C] 백준 | 2164번 코드 - 카드2 (0) | 2021.02.27 |
| [C] 백준 | 1978번 코드 - 소수찾기 (0) | 2021.02.24 |
| [C] 백준 | 1920번 코드 - 수 찾기 (0) | 2021.02.24 |
| [C] 백준 | 11650, 11651번 코드 - 좌표 정렬하기1, 2 (0) | 2021.02.24 |
