티스토리 뷰
https://www.acmicpc.net/problem/1707
1707번: 이분 그래프
입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V와 간선의 개수 E가 빈 칸을 사이에
www.acmicpc.net
import java.io.*;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
static ArrayList<ArrayList<Integer>> list = new ArrayList<>(); // 인접리스트
static int[] color; // 정점의 색 정보 담을 배열
static boolean checkBip; // 이분 그래프 유무 체크
public static boolean bfs(int idx) {
Queue<Integer> queue = new LinkedList<>();
queue.add(idx);
color[idx] = 1;
while(!queue.isEmpty()) {
int e = queue.poll();
for(int adjV : list.get(e)) {
// 방문하지 않은 정점이면
if(color[adjV] == 0) {
color[adjV] = color[e] * -1;
queue.add(adjV);
}
// 방문한 정점인데, 겹치는 색이 있는 경우는 이분그래프가 아니다
// (-1 + 1 == 0)이 되어야 정상.
else if(color[adjV] + color[e] != 0) {
return false;
}
}
}
return true;
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer stk;
int T = Integer.parseInt(br.readLine());
for(int t = 0; t < T; t++) {
// 데이터 입력 및 인접리스트 생성
list.clear(); // 초기화 필수!
checkBip = true; // 초기화
stk = new StringTokenizer(br.readLine());
int V = Integer.parseInt(stk.nextToken());
int E = Integer.parseInt(stk.nextToken());
color = new int[V + 1]; // 1번부터 시작하게
for(int i = 0; i <= V; i++) {
list.add(new ArrayList<Integer>());
}
for(int i = 0; i < E; i++) {
stk = new StringTokenizer(br.readLine());
int a = Integer.parseInt(stk.nextToken());
int b = Integer.parseInt(stk.nextToken());
list.get(a).add(b);
list.get(b).add(a);
}
for(int i = 1; i <= V; i++) {
if(color[i] == 0) {
checkBip = bfs(i);
}
if(!checkBip) {
break;
}
}
bw.write(checkBip ? "YES" : "NO");
bw.newLine();
}
bw.flush();
bw.close();
}
}이분 그래프 문제
어려웠다. 다른 사람 코드 참조를 할 수밖에 없었는데, 안그랬다면 평생 못풀었을 것 같다.
이분그래프를 나누라고 하길래 일단 부분집합을 두개 나눠야햐나 그럼 어떻게 나누지 이 생각 하고 있었는데
이 문제는 그런 방식으로 푸는 문제가 아니었던 것이다...!!!

"그래프 이론에서, 이분 그래프(二分graph, 영어: bipartite graph)란 모든 꼭짓점을 빨강과 파랑으로 색칠하되, 모든 변이 빨강과 파랑 꼭짓점을 포함하도록 색칠할 수 있는 그래프이다." <위키피디아>
위와 같이 모든 정점을 두가지 색으로 색칠하되.
같은 색으로 색칠된 정점끼리는 서로 인접하지 않는 그래프를 이분 그래프라고 한다.
BFS로 이분 그래프를 어떻게 찾을 수 있는지 알아보자
1. 1번 정점에서부터 탐색 시작. 1번 정점을 빨간색으로 칠하고, 큐에 넣는다
2. 큐에서 팝. 1번 정점에서 인접한 정점(2번)의 색을 파랑색으로 칠하고, 큐에 넣는다
3. 큐에서 팝. 2번 정점에서 인접한 정점(3, 4번)의 색을 빨간색으로 칠하고, 큐에 넣는다
4. 큐에서 팝. 3번 정점에서 인접한 정점(2, 4번)이 있는데 이미 둘다 색칠이 되어있는 상태.
- 3번 정점의 색이 빨간색이므로, 3번과 인접한 정점의 색은 파랑색이어야 하는데, 4번 정점의 색이 이미 빨간색으로 칠해져 있음. -> 이는 이분그래프가 아니라는 의미이므로 바로 탐색 종료.
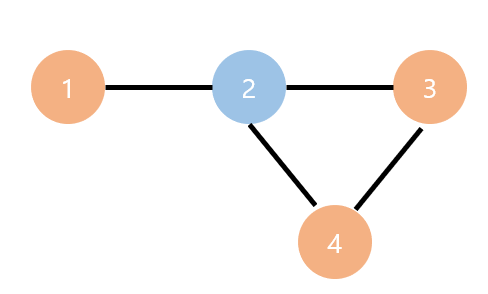
대충 이런 상황이다
# 정점의 색칠은 빨강은 1, 파랑은 -1 으로 잡아서 현재 정점에서 * -1 만 해줌으로써 쉽게 바꿀 수 있도록 한다.
if(color[adjV] == 0) {
color[adjV] = color[e] * -1;
queue.add(adjV);
}# 인접 정점과 색이 같은지 체크하는 방법
else if(color[adjV] + color[e] != 0) {
return false;
}color[adjV]가 빨강(1) 이라고 하면, color[e] 는 파랑(-1)이어야 정상적인 이분그래프이다.
이 두개를 더했을 때 0이 되지 않는다면 파랑+파랑, 빨강+빨강이라는 뜻이므로 이분그래프가 아님을 알 수 있다
(둘다 이미 방문한 정점이라는 것을 체크한 후에)
또 유의해야할 점은, 모든 정점이 서로 연결되어 있을거라는 보장이 없다는 것..;;
아무와도 연결되어있지 않은 정점이 있을 수도 있는 것이다
그래서 모든 정점에서 다 탐색해봐야 한다.

이런건 모르면 손도 못대던가 개고생해서 겨우 풀 수있는 문제인 것 같다..
많이 풀어보는게 답이겠지......
'알고리즘 > BFS & DFS & 백트래킹' 카테고리의 다른 글
| [JAVA] # 1261 알고스팟 (0) | 2021.09.03 |
|---|---|
| [JAVA] 다익스트라 알고리즘 기본 틀 (#5972 택배배송) (0) | 2021.09.03 |
| [JAVA] # 13549 숨바꼭질 3 (0) | 2021.08.26 |
| [JAVA] #14226 이모티콘 (0) | 2021.08.26 |
| [JAVA] #4963 섬의 개수 (0) | 2021.08.24 |
