티스토리 뷰
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
static final int INF = 999999999;
static int sum = 0;
static List<List<Node>> graph = new ArrayList<>();
static int[] distance;
static boolean[] visited;
static class Node implements Comparable<Node> {
int idx;
int dist;
Node(int idx, int dist) {
this.idx = idx;
this.dist = dist;
}
@Override
public int compareTo(Node o) {
return this.dist - o.dist;
}
}
public static void dijkstra(int start) {
PriorityQueue<Node> queue = new PriorityQueue<>();
distance[start] = 0;
queue.add(new Node(start, 0));
while(!queue.isEmpty()) {
Node e = queue.poll();
if(visited[e.idx]) {
continue;
}
visited[e.idx] = true;
for (Node linkedNode : graph.get(e.idx)) {
if(e.dist + linkedNode.dist < distance[linkedNode.idx]) {
distance[linkedNode.idx] = e.dist + linkedNode.dist;
queue.add(new Node(linkedNode.idx, distance[linkedNode.idx]));
sum += linkedNode.dist;
}
}
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer stk = new StringTokenizer(br.readLine());
int N = Integer.parseInt(stk.nextToken());
int M = Integer.parseInt(stk.nextToken());
for(int i = 0; i < N; i++) {
graph.add(new LinkedList<>());
}
distance = new int[N];
visited = new boolean[N];
Arrays.fill(distance, INF);
for(int i = 0; i < M; i++) {
stk = new StringTokenizer(br.readLine());
int u = Integer.parseInt(stk.nextToken());
int v = Integer.parseInt(stk.nextToken());
int w = Integer.parseInt(stk.nextToken());
graph.get(u - 1).add(new Node(v - 1, w));
graph.get(v - 1).add(new Node(u - 1, w));
}
dijkstra(0);
System.out.println(distance[N - 1]);
}
}그 이름도 유명한 다익스트라 알고리즘이다
작동 알고리즘을 한번 알아보자..


다음과 같은 양방향 그래프가 있다고 생각해 보자. 1번 노드부터 탐색을 시작한다.
1번 노드와 2번 4번 노드가 연결되어있기 때문에 최단경로를 업데이트 해준다

이후, 방문하지 않은 노드 중에서 가장 가중치가 낮은 노드로 이동한다

이후, 2번 노드에서 갈 수 있는 4번, 3번 노드의 최단경로를 업데이트 한다
위와 같은 과정의 반복이다.

2번노드에서 갈 수 있는 최단노드인 4번 노드로 이동 후 업데이트 반복

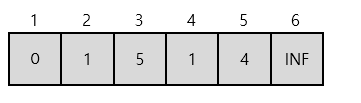
5번노드로 이동
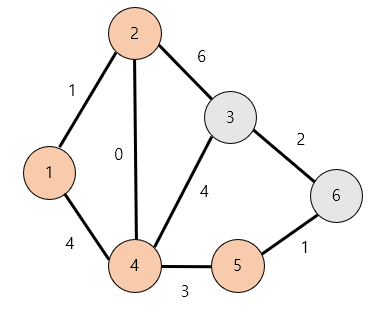
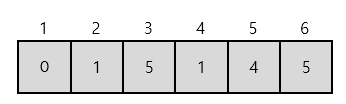
6번노드로 이동
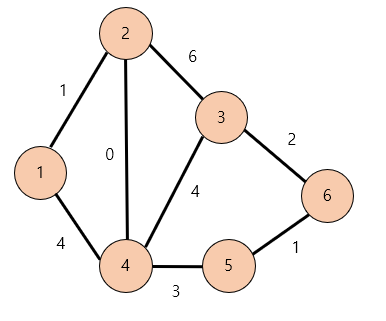
3번노드로 이동 -> 모든 노드를 방문했다!

비로소 우리는 가중치가 있는 그래프에서 1번 노드에서 출발했을때 N번 노드로 도착할 수 있는 최단 거리를 구할 수 있게 되었다.
* 다익스트라 알고리즘은 여러개의 최단거리를 이어붙여 최단거리를 구하기 때문에
다이나믹 프로그래밍 / 그리디 알고리즘 타입이기도 하다
* 다익스트라 알고리즘은 "음의 가중치"가 있는 경우는 최단경로를 보장하지 않는다.
* 시간 복잡도는 O((V+E)logV) - (연결리스트 + 우선순위 큐 사용한 경우).
* 알고리즘의 증명은 수학적 귀납법을 통해서 검증하는데,, 이하 생략

이론은 대충 뭔소리를 지껄이는지 이해가 되는 것 같은데,
이걸 구현을 하라고 하니 갑자기 가슴이 답답해지고 손발이 떨려온다.
어떻게 해야할까?
코드를 살펴보자..
우선 각 노드의 정보(인덱스, 가중치값)을 담을 Node 클래스를 만들어보자
static class Node implements Comparable<Node> {
int idx; // "도착 노드"의 인덱스
int dist; // 가중치
Node(int idx, int dist) { // 생성자
this.idx = idx;
this.dist = dist;
}
// "우선순위 큐"를 사용하기 위한 compareTo 오버라이드
// dist를 기준으로 오름차순 정렬한다.
@Override
public int compareTo(Node o) {
return this.dist - o.dist;
}
}난데없는 Comparable 인터페이스의 등장에 굉장히 당혹스러울 따름이다.
이는 우선순위 큐를 사용하기 위해 필요하다.
(가중치를 기준으로 오름차순 정렬... 가중치가 제일 낮은 노드가 맨 앞에 오도록 세팅한다)
-> 현재 노드에서 제일 가중치가 낮은 노드로 쉽게 이동하기 위함
** Node 클래스의 idx 변수는 "도착 노드"의 인덱스 정보를 담는다!! 헷갈리지 말기
==
객체를 정렬하는 방법은 두가지가 있다.
1. Comparable 인터페이스를 활용하기 - compareTo() 메소드를 오버라이드 하여 내가 원하는 정렬기준을 작성.
2. Comparator 인터페이스를 활용하기 - 주로 "익명 클래스" 로 활용한다 - compare() 메소드를 오버라이드.
두개의 차이는
Comparable은 자기자신과 매개변수1 객체를 비교한다는 것과
Comparator는 매개변수1 객체와 매개변수2 객체를 비교한다는 점이다.
==
다음으로는 main 메소드
// static List<List<Node>> graph = new ArrayList<>();
// static final int INF = 999999999;
//
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer stk = new StringTokenizer(br.readLine());
// 데이터 입력 및 배열 초기화
int N = Integer.parseInt(stk.nextToken());
int M = Integer.parseInt(stk.nextToken());
for(int i = 0; i < N; i++) {
graph.add(new LinkedList<>());
}
distance = new int[N]; // 최단거리를 담아놓을 배열
visited = new boolean[N]; // 방문여부 체크
Arrays.fill(distance, INF); // 최단거리 배열은 INF로 초기화한다.
// 연결 그래프 생성
// u - 1, v - 1을 하는 이유 => 0번 인덱스부터 시작하기 위함
for(int i = 0; i < M; i++) {
stk = new StringTokenizer(br.readLine());
int u = Integer.parseInt(stk.nextToken()); // 출발점
int v = Integer.parseInt(stk.nextToken()); // 도착점
int w = Integer.parseInt(stk.nextToken()); // 가중치
graph.get(u - 1).add(new Node(v - 1, w)); // "양방향" 그래프
graph.get(v - 1).add(new Node(u - 1, w)); // "양방향" 그래프
}
dijkstra(0); // K번 노드부터 탐색을 시작
System.out.println(distance[N - 1]);
}
최단거리 정보를 저장할 distance 배열은 INF로 초기화를 해두어야 한다!
INF는 static final을 이용하여 엄청 큰 수로 세팅해둔다.
* INF를 Integer.MAX_VALUE로 설정하면 추후 최단거리 비교를 할때 오버플로우가 발생하게 된다
대충 융통성 있게 세팅할것! 알잘딱깔센
이제 대망의 다익스트라 알고리즘
public static void dijkstra(int start) {
PriorityQueue<Node> queue = new PriorityQueue<>(); // 우선순위큐
distance[start] = 0;
queue.add(new Node(start, 0));
while(!queue.isEmpty()) {
Node e = queue.poll();
if(visited[e.idx]) { // 이미 방문한 정점이면 더 볼필요가 없음
continue;
}
visited[e.idx] = true;
// 핵심
for (Node linkedNode : graph.get(e.idx)) {
if(e.dist + linkedNode.dist < distance[linkedNode.idx]) {
distance[linkedNode.idx] = e.dist + linkedNode.dist;
queue.add(new Node(linkedNode.idx, distance[linkedNode.idx]));
sum += linkedNode.dist;
}
}
}
}우선순위 큐를 사용한다. 최단거리 정점을 쉽게 찾아가기 위함.
핵심은 최단경로를 갱신하는 파트에 있다.
우선 현재 노드와 연결된 모든 노드들을 for문을 활용해 탐색한다.

e.idx = 1
e.dist = 0
linkedNode.idx = 2
linkedNode.dist = 1
* (Node 클래스는 도착 노드의 인덱스, 거리를 담고 있다 했으니까!)
e.dist + linkedNode.dist < distance[linkedNode.idx]를 하면 0 + 1 < INF이므로, 최단경로가 갱신이 됨을 알 수 있다.
이 경우에
distance[linkedNode.idx] = e.dist + linkedNode.dist;
queue.add(new Node(linkedNode.idx, distance[linkedNode.idx]));배열을 갱신하고, 큐에 넣는다.
큐에는 다음에 이동할 인덱스와 가중치를 노드로 생성하여 담는다

반복문을 다 돌고 나면 우선순위 큐에는 <<-{ (idx:2, dist:1), (idx:4, dist:4) }-- 순으로 배치가 되어 있을 것이다.
그러므로 2번 노드로 이동한다

e.idx = 2
e.dist = 1
linkedNode.idx = 4
linkedNode.dist = 0
1 + 0 < 4 이므로 최단경로가 갱신이 됨을 알 수 있다!!
반복문을 다 돌고 나면 다음과 같은 배열이 갱신 될 것이다.

큐에는 <<-{ (idx:4, dist:1), (idx:4, dist:4), (idx:3, dist:7) }-- 순으로 배열이 되어있을 것이다.
따라서 4번 노드로 이동하고 위와같은 과정의 반복이다
그리고 잘 보면 알겠지만 한번 방문한 노드는 두번다시 볼 필요가 없다.
visited 체크로 큐에서 (idx:4, dist:4) 같은게 팝 되었을때는 그냥 무시하고 바로 continue 때릴 수 있도록 해준다.
그럼 끝!
'알고리즘 > BFS & DFS & 백트래킹' 카테고리의 다른 글
| [JAVA] # 3055 탈출 (0) | 2021.09.07 |
|---|---|
| [JAVA] # 1261 알고스팟 (0) | 2021.09.03 |
| [JAVA] #1707 이분그래프 * (0) | 2021.09.02 |
| [JAVA] # 13549 숨바꼭질 3 (0) | 2021.08.26 |
| [JAVA] #14226 이모티콘 (0) | 2021.08.26 |
